Рисуване с помощта на цикли¶
Помислете за следната задача: нека нарисуваме 6 кръга, както е на тази снимка:
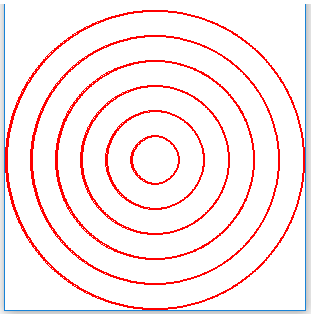
Разглеждайки снимката, можем да предположим (или би могло да се каже в проблемната настройка), че кръговете са еднакво разположени. Това означава, че разликата в радиуса на всеки два съседни кръга е една и съща.
Избираме размера на кръговете да е възможно най-голям, но да се побере в дадено чертожно пространство от 300x300 пиксела. Тъй като ширината на прозореца е 300 пиксела, радиусът на най-големия кръг е 150. За разликата на радиусите на двете съседни кръгове можем да вземем \({150 \ over 6} = 25\). Това дава радиуси от 25, 50, 75, 100, 125, 150.
Въз основа на изчислените стойности можем да напишем програма като тази:
Нека си представим, че след това ни беше дадена новата задача да направим същата рисунка, но с 5 кръга. Това е много малка промяна, нали? Трябва да можем да използваме повторно решената по-рано задача.
Когато започнем да работим върху рисунка с 5 кръга, виждаме, че може да се използва много малко от предишната програма. Всъщност можем да използваме само идеята и размерът на кръговете трябва да се изчислява от нулата.
Ако бяхме написали програмата по различен начин, персонализирането й щеше да бъде много по-лесно. Можем например да запишем броя на кръговете в променлива и след това да използваме тази променлива при всички необходими изчисления. Тази програма ще изглежда така:
В тази програма е достатъчно да промените само едно число, така че да нарисува произволен брой кръгове.
Както казахме по-рано, много рисунки имат някаква закономерност, като симетрия или някаква повтаряща се част (и много други, по-сложни модели). Ако разберем закономерността на такива рисунки и я изразим математически, ще можем да я използваме, когато пишем програма за изготвяне на такива рисунки, както направихме в предишния пример. По този начин получаваме програма, която е много по-лесно да се модифицира, за да се получи друга, подобна рисунка. За рисунки с голям брой повторения на част (идентични или леко модифицирани) програмата, която използва редовност, също ще бъде много по-къса.
Много програми, използвани от милиони хора, непрекъснато се усъвършенстват и усъвършенстват и се публикуват нови версии на такива програми. Следователно промените в програмата са нещо напълно нормално, което се случва непрекъснато. Подобна е ситуацията и с програмите, които сами пишем. Когато пишем програма, лесно може да се случи, че по-късно мислим за нещо ново и искаме да модифицираме част от програмата, която вече е написана.
Ето защо, когато пишем програми, трябва да имаме предвид, че някой (вероятно сами) ще иска да създаде подобна програма и може да иска да използва програмата ни като първоначална версия.
Нека да разгледаме друг пример как можем да използваме закономерностите в чертежа, за да напишем по-гъвкава програма (програма, която е по-лесна за адаптиране към малко по-различна цел).
Пример - антена¶
Вече видяхме програма, която рисува тази антена. Сега програмата е написана така, че да не е твърде трудно да промените броя на напречните сегменти, разстоянието между тях, разликата в дължините на последователни сегменти и други подобни.
Част от програмата, която рисува напречните сегменти на антената, може да бъде написана, както следва:
for i in range(6):
pg.draw.line(canvas, pg.Color('darkgray'), (120 - 10 * i, 75 + 25 * i), (180 + 10 * i, 75 + 25 * i), 1 + i//2)
Програмата, написана по този начин, би била малко по-къса, но първата е по-ясна, така че всяка има своите предимства. Нека само да отбележим, че и двете програми са по-добри, отколкото да рисуваме по 6 линии един по един за напречни сегменти (ние преди това). Ако тази част от програмата се състоеше от шест обаждания към функцията за изтегляне на линия, би било по-трудно да се модифицира и коригира програмата, за да се очертае различна антена.
Равнопоставени числа¶
И в двата предишни примера беше необходимо да се изброят една или повече серии от еднакви разстояния. В задачата с кръгове това бяха числа 25, 50, 75, 100, 125, 150 (радиуси на кръгове), а в задачата с антената ни бяха нужни колкото четири серии от числа - x и y координати на краищата на напречните сегменти на антената. По-специално, тези числа са:
x coordinates of left ends: 120, 110, 100, 90, 80, 70
y coordinates of left ends: 75, 100, 125, 150, 175, 200
x coordinates of right ends: 180, 190, 200, 210, 220, 230
y coordinates of right ends: 75, 100, 125, 150, 175, 200
Видяхме, че има различни начини да получим ценностите, от които се нуждаем. Например в задача с концентрични кръгове, стойности 25, 50, 75, 100, 125, 150, бихме могли да получим по някой от следните (еднакво добри) начини:
for r in range(25, 151, 25):
pg.draw.circle(canvas, pg.Color("red"), center, r, 2)
for i in range(br_krugova):
pg.draw.circle(canvas, pg.Color("red"), center, round(25 + i * 25), 2)
r = 25
for _ in range(br_krugova):
pg.draw.circle(canvas, pg.Color("red"), center, r, 2)
r += 25
В общия случай, ако трябва да получим поредица от стойности на a, a+d, a+2d, … a+(n-1)d, предишните три метода могат да бъдат използва се както следва:
for x in range(a, a + n*d, d):
print(x)
for i in range(n):
print(a+i*d)
x = a
for _ in range(n):
print(x)
x += d
Ще видим, че много задачи с рисуване на еднакви дистанционни форми могат да бъдат решени чрез прилагане на контури като тази.
Обърнете внимание, че функцията range със стъпка (с три аргумента) трябва да получава цели аргументи, така че в ситуации, в които стъпката не е цяло число, нейното използване не е възможно.
Когато имаме нужда (както при задаване на антена) да направим няколко серии в един цикъл, първият режим е по-малко удобен, така че трябва да изберем един от другите два начина.
Следващите въпроси ще ви помогнат да затвърдите знанията си за формиране на серия от еднакви разстояния от числа.
-
Q-63: Съберете серия от числа с цикъла, който ги е генерирал.
try again!
- 100, 200, 300, 400, 500
- for i in range(100, 600, 100)
- 100, 300, 500
- for i in range(100, 601, 200)
- 100, 200, 300, 400, 500, 600
- for i in range(100, 601, 100)
- 200, 300, 400, 500, 600
- for i in range(200, 601, 100)
-
Q-64: Съпоставете получените числа с израза "for i in range (5):" с цикъла, който ги генерира.
try again!
- 100, 150, 200, 250, 300
- x = 100 + i*50
- 50, 150, 250, 350, 450
- x = 50 + i*100
- 0, 100, 200, 300, 400
- x = i*100
- 100, 200, 300, 400, 500
- x = 100+i*100
- x = 25 * i + 50
- No.
- x = (25 + i) * 50
- No.
- x = 25 * 2*i+1
- No.
- x = 25 + 50 * i
- Correct!
Q-65: Кое трябва да бъде използвано в цикъла.
for i in range(19):
x = ???
...
за да има x същата стойност, както в цикъла
for x in range(25, 500, 50):
...
Задачите за упражнение са следните.
Стълба¶
Променете програмата така, че стъпалата на стълбата да бъдат очертани в цикъл.
Вместо 5 редови извода за рисуване, можете да използвате цикъл от следната форма:
for y in ???:
pg.draw.line(canvas, pg.Color("brown"), (100, y), (200, y), 10)
To complete the loop correctly, you need to answer the following question:
- range(0, 50, 250)
- No, the first number is not appropriate for that range.
- range(250, 50)
- No, try again.
- range(50, 251, 50)
- Correct!
- range(50, 250, 50)
- No, the last number is not appropriate for that range.
Q-66: Which of the ranges offered gives values 50, 100, 150, 200, 250?
Дървета¶
Променете програмата така, че едно дърво да бъде нарисувано във всяко или трите преминавания през цикъла.
Програмата би изглеждала така:
при което вместо въпросните знаци трябва да се поставят подходящи изрази за координатата x. Когато i приема стойностите 0, 1, 2 в ред, изразът в първия израз трябва да приема стойностите 40, 140, 240, а изразът във втория израз трябва да приема стойностите 10, 110, 210.
Решетка¶
Променете програмата така, че вертикалните линии да бъдат начертани в един цикъл, а хоризонталните линии във втория.